Compito A del 7-04-05. Domande teoria.
DOMANDA 1 (punti 6)
Specificare i vari passaggi necessari per la conversione del numero 123.25
in base 10 nella rappresentazione binaria. Usare 8 bit per la parte intera
e 4 bit per la parte frazionaria.
DOMANDA 2 (punti 6)
Elencare e spiegare i cinque diversi modi di indirizzamento della macchina
MIPS.
DOMANDA 3 (punti 6)
Dire qualè la complessità temporale dellalgoritmo di Dijkstra per la
determinazione dellalbero dei cammini minimi in un grafo G connesso, non
orientato e pesato con pesi non negativi. Ipotizzare una rappresentazione
del grafo mediante lista delle adiacenze e una rappresentazione dellADT
coda mediante heap. Motivare la risposta.
DOMANDA 4 (punti 6)
Dato un grafo G(V,E) orientato, dimostrare che se G è aciclico allora deve
avere almeno un vertice con in-degree (numero archi entranti) eguale a zero.
Compito B del 7-04-05. Domande teoria.
DOMANDA 1 (punti 6)
Specificare i vari passaggi necessari per la conversione del numero 101.75
in base 10 nella rappresentazione binaria. Usare 8 bit per la parte intera
e 4 bit per la parte frazionaria.
DOMANDA 2 (punti 6)
Illustrare le convenzioni che regolano in MIPS luso dei registri nelle
procedure ricorsive.
DOMANDA 3 (punti 6)
Discutere la complessità temporale dellalgoritmo di Prim per la
determinazione del Minimum Spanning Tree di un grafo G connesso, non
orientato e pesato. Ipotizzare una rappresentazione del grafo mediante
lista delle adiacenze e una rappresentazione dellADT coda mediante heap.
Motivare la risposta.
DOMANDA 4 (punti 6)
Dato un grafo G connesso e pesato. Supposta una partizione dei vertici di
G nei due sottoinsiemi disgiunti e non vuoti V1 e V2. Supposto, inoltre,
essere e un arco avente peso minimo tra quelli che attraversano la
partizione. Dimostrare che, in tali ipotesi, esiste un Minimum Spanning
Tree contenente larco e.
DOMANDA 5 (punti 6)
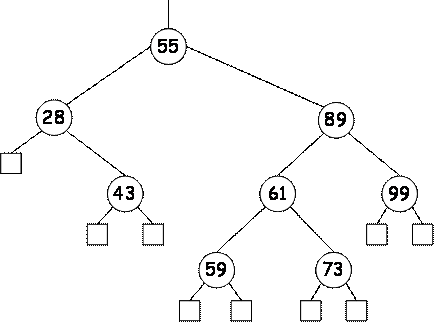
Illustrare graficamente, spiegando dettagliatamente lalgoritmo nei suoi i
vari passaggi e ridisegnando di volta in volta lalbero, la rimozione del
valore 43 nellalbero AVL di seguito riportato.
