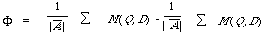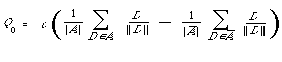The iterative procedure is called the fixed-increment error correction procedure.

It goes as follows:

Qi = Qi-1 + cD if M(Qi-1, D) - T <= 0

and D [[propersubset]] A

Qi = Qi-1 - cD if M(Qi-1, D) - T > 0

and D [[propersubset]] `A

and no change made to Qi-1 if it diagnoses correctly. c is the correction increment, its value is arbitrary and is therefore usually set to unit. In practice it may be necessary to cycle through the set of documents several times before the correct set of weights are achieved, namely those which will separate A and `A linearly (this is always providing a solution exists).

The situation in actual retrieval is not as simple. We do not know the sets A and `A in advance, in fact A is the set we hope to retrieve. However, given a query formulation Q and the documents retrieved by it we can ask the user to tell the system which of the documents retrieved were relevant and which were not. The system can then automatically modify Q so that at least it will be able to diagnose correctly those documents that the user has seen. The assumption is that this will improve retrieval on the next run by virtue of the fact that its performance is better on a sample.

Once again this is not the whole story. It is often difficult to fix the threshold T in advance so that instead documents are ranked in decreasing matching value on output. It is now more difficult to define what is meant by an ideal query formulation. Rocchio[15] in his thesis defined the optimal query Q0 as one which maximised:

If M is taken to be the cosine function (Q, D) /||Q || ||D || then it is easy to show that [[Phi]] is maximised by

where c is an arbitrary proportionality constant.