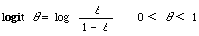Using the logit transformation for probabilities, that is

the basic quantitative model for a single query j they propose is

logit [[theta]]j1 = [[alpha]]j + [[Delta]]j

logit [[theta]]j2 = [[alpha]]j - [[Delta]]j

Here [[theta]]j1 and [[theta]]j2 are probabilities corresponding to recall and fallout respectively as defined in the previous section. The parameters [[alpha]]j and [[Delta]]j are to be interpreted as follows:

[[alpha]]j measures the specificity of the query formulation; [[Delta]]j measures the separation

of relevant and non-relevant documents.

For a given query j if the query i has been formulated in a more specific way than j, one would expect the recall and fallout to decrease, i.e.

[[theta]]i1 < [[theta]]j1 and [[theta]]i2 < [[theta]]j2

Also, if for query i the system is better at separating the non-relevant from the relevant documents than it is for query j one would expect the recall to increase and the fallout to decrease, i.e.

[[theta]]i1 > [[theta]]j1 and [[theta]]i2 < [[theta]]j2

Given that logit is a monotonic transformation, these interpretations are consistent with the simple quantitative model defined above.

To arrive at an estimation procedure for [[alpha]]j and [[Delta]]j is a difficult technical problem and the interested reader should consult Robertson's thesis[19]. It requires certain assumptions to be made about [[alpha]]j and [[Delta]]j , the most important of which is that the {[[alpha]]j }and {[[Delta]]j }are independent and normally distributed. These assumptions are rather difficult to validate. The only evidence produced so far derives the distribution of {[[alpha]]j } for certain test data. Unfortunately, these estimates, although they are unimodally and symmetrically distributed themselves, can only be arrived at by using the normality assumption. In the case of [[Delta]]j it has been found that it is approximately constant across queries so that a common-[[Delta]] model is not unreasonable:

logit [[theta]]j1 = [[alpha]]j1 + [[Delta]]

logit [[theta]]j2 = [[alpha]]j2 - [[Delta]]

From them it would appear that [[Delta]] could be a candidate for a single number measure of effectiveness. However, Robertson has gone to some pains to warn against this. His main argument is that these parameters are related to thebehavioural characteristics of an IR