assume that we have the points on l1 and l2 a but wish to deduce the relative ordering in between these two lines. One may think of this as an interpolation procedure.

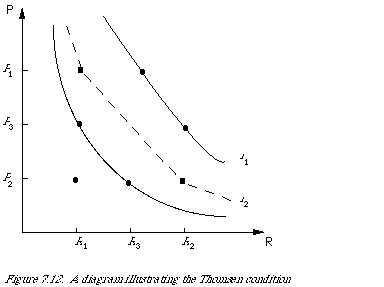
Definition 3 (Thomsen condition). For every R1, R2 , R3 [[propersubset]] R and P1, P2, P3 [[propersubset]] P, (R1, P3) ~ (R3, P 2) and (R3, P1) ~ (R2, P 3) imply that (R1, P1) ~ (R2, P 2).

Intuitively this can b e reasoned as follows. The intervals R1 R3 and P2 P 3 are equivalent since an increase in the R-factor by R1 R3 and an increase in the P-factor by P2 P3 starting from (R1 , P3) lead to the same effectiveness (points on l2). It therefore follows that a decrease in each factor starting from equal effectiveness, in this case the two points (R3, R1) and (R2 , P3) on l1, should lead to equal effectiveness.

The fourth condition is one concerned with the continuity of each component. It makes precise what intuitively we would expect when considering the existence of intermediate values.

Definition 4 (Restricted Solvability). A relation >= on R x P satisfies restricted solvability provided that:

(1) whenever R, `R, R [[propersubset]] R and P, P' [[propersubset]] P for which (`R, P') >= (R, P) >= (R, P') then there exists R [[propersubset]] R s.t. (R, P') ~ (R, P);

(2) a similar condition holds on the second component.