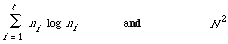where n1 < n2 < . . . < nt = N, and t is the number of updates. In the limit when n is a continuous variable and the sum becomes an integral we are better off with N^2. In the discrete case the comparison depends rather on the size of the updates ni - ni - 1. So unless we can design an n log n dependence as extra documents are added, we may as well stick with the n^2 methods which satisfy the soundness conditions and preserve n^2 dependence during updating.

In any case, if one is willing to forego some of the theoretical adequacy conditions then it is possible to modify the n^2 methods to 'break the n^2 barrier'. One method is to sample from the document collection and construct a core clustering using an n^2 method on the sample of the documents. The remainder of the documents can then be fitted into the core clustering by a very fast assignment strategy, similar to a search strategy which has log n dependence. A second method is to initially do a coarse clustering of the document collection and then apply the finer classification method of the n^2 kind to each cluster in turn. So, if there are N documents and we divide into k coarse clusters by a method that has order N time dependence (e.g. Rieber and Marathe's method) then the total cluster time will be of order N + [[Sigma]] (N/k)^2 which will be less than N[2].

Another comment to be made about n log n methods is that although they have this time dependence in theory, examination of a number of the algorithms implementing them shows that they actually have an n^2 dependence (e.g. Rocchio's algorithm). Furthermore, most n log n methods have only been tested on single-level classifications and it is doubtful whether they would be able to preserve their n log n dependence if they were used to generate hierarchic classifications (Senko[54]).

In experiments where we are often dealing with only a few thousand documents, we may find that the proportionality constant in the n log n method is so large that the actual time taken for clustering is greater than that for an n^2 method. Croft[55] recently found this when he compared the efficiency of SNOB (Boulton and Wallace[56]), an n log n cluster method, with single-link. In fact, it is possible to implement single-link in such a way that the generation of the similarity values is overlapped in real time with the cluster generation process.

The implementation of classification algorithms for use in IR is by necessity different from implementations in other fields such as for example numerical taxonomy. The major differences arise from