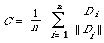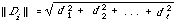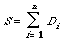that their corresponding documents are less dissimilar than some specified level of dissimilarity. Now, one way of representing a cluster is to select a typical member from the cluster. A simple way of doing this is to find that document which is linked to the maximum number of other documents in the cluster. A suitable name for this kind of cluster representative is the maximally linked document. In the clusters A and B illustrated, there are pointers to the candidates. As one would expect in some cases the representative is not unique. For example, in cluster B we have two candidates. To deal with this, one either makes an arbitrary choice or one maintains a list of cluster representatives for that cluster. The motivation leading to this particular choice of cluster representative is given in some detail in van Rijsbergen[3] but need not concern us here.

Let us now look at other ways of representing clusters. We seek a method of representation which in some way 'averages' the descriptions of the members of the clusters. The method that immediately springs to mind is one in which one calculates the centroid (or centre of gravity) of the cluster. If {D1, D2, . . ., Dn} are the documents in the cluster and each Di is represented by a numerical vector (d1, d2, . . ., dt) then the centroid C of the cluster is given by

where ||Di|| is usually the Euclidean norm, i.e.

More often than not the documents are not represented by numerical vectors but by binary vectors (or equivalently, sets of keywords). In that case we can still use a centroid type of cluster representative but the normalisation is replaced with a process which thresholds the components of the sum [[Sigma]]Di. To be more precise, let Di now be a binary vector, such that a 1 in the jth position indicates the presence of the jth keyword in the document and a 0 indicates the contrary. The cluster representative is now derived from the sum vector

(remember n is the number of documents in the cluster) by the following procedure. Let C = (c1, c2, . . . ct) be the cluster