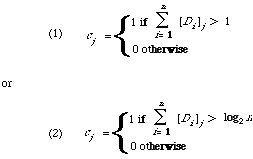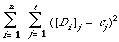So, finally we obtain as a cluster representative a binary vector C. In both cases the intuition is that keywords occurring only once in the cluster should be ignored. In the second case we also normalise out the size n of the cluster.

There is some evidence to show that both these methods of representation are effective when used in conjunction with appropriate search strategies (see, for example, van Rijsbergen[4] and Murray[5]). Obviously there are further variations on obtaining cluster representatives but as in the case of association measures it seems unlikely that retrieval effectiveness will change very much by varying the cluster representatives. It is more likely that the way the data in the cluster representative is used by the search strategy will have a larger effect.

There is another theoretical way of looking at the construction of cluster representatives and that is through the notion of a maximal predictor for a cluster[6]. Given that, as before, the documents Di in a cluster are binary vectors then a binary cluster representative for this cluster is a predictor in the sense that each component (ci) predicts that the most likely value of that attribute in the member documents. It is maximal if its correct predictions are as numerous as possible. If one assumes that each member of a cluster of documents D1, . . ., Dn is equally likely then the expected total number of incorrect predicted properties (or simply the expected total number of mismatches between cluster representative and member documents since everything in binary) is,