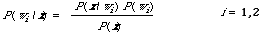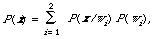Since we are assuming that each document is described by the presence/absence of index terms any document can be represented by a binary vector,

x = (x1,x2, . . ., xn)

where xi = 0 or 1 indicates absence or presence of the ith index term. We also assume that there are two mutually exclusive events,

w1 = document is relevant

w2 = document is non-relevant.

* The theory that follows is at first rather abstract, the reader is asked to bear with it, since we soon return to the

nuts and bolts of retrieval.

So, in terms of these symbols, what we wish to calculate for each document is P(w1/x) and perhaps P(w2/x) so that we may decide which is relevant and which is non-relevant. This is a slight change in objective from simply producing a ranking, we also wish the theory to tell us how to cut off the ranking. Therefore we formulate the problem as a decision problem. Of course we cannot estimate P(wi/x) directly so we must find a way of estimating it in terms of quantities we do know something about. Bayes' Theorem tells us that for discrete distributions

Here P(wi) is the prior probability of relevance (i=1) or non-relevance (i=2), P(x/wi) is proportional to what is commonly known as the likelihood of relevance or non-relevance given x; in the continuous case this would be a density function and we would write p(x/wi). Finally,

which is the probability of observing x on a random basis given that it may be either relevant or non-relevant. Again this would be written as a density function p(x) in the continuous case. although P(x) (or p(x) ) will mostly appear as a normalising factor (i.e. ensuring that P(w1/x) + P(w2/x) = 1) it is in some ways the function we know most about, it does not require a knowledge of relevance for it to be specified. Before I discuss how we go about estimating the right hand side ofBayes' Theorem I will show how the decision for or against relevanceis made.