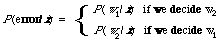The decision rule we use is in fact well known as Bayes' Decision Rule. It is

[P (w1/x) > P(w2/x) -> x is relevant, x is non-relevant] * D1

The expression D1 is a short hand notation for the following: compare P (w1/x) with P(w2/x) if the first is greater than the second then decide that x is relevant otherwise decide x is non-relevant. The case P(w1/x) = P(w2/x) is arbitrarily dealt with by deciding non-relevance. The basis for the rule D1 is simply that it minimises the average probability of error, the error of assigning a relevant document as non-relevant or vice versa. To see this note that for any x the probability of error is

* The meaning of [E -> p,q] is that if E is true then decide p, otherwise decide q.

In other words once we have decided one way (e.g. relevant) then the probability of having made an error is clearly given by the probability of the opposite way being the case (e.g. non-relevant). So to make this error as small as possible for any given x we must always pick that wi for which P (w1/x) is largest and by implication for which the probability of error is the smallest. To minimise the average probability of error we must minimise

This sum will be minimised by making P (error/x) as small as possible for each x since P(error/x) and P(x) are always positive. This is accomplished by the decision rule D1 which now stands as justified.

Of course average error is not the only sensible quantity worth minimising. If we associate with each type of error a cost we can derive a decision rule which will minimise the overall risk. The overall risk is an average of the conditional risks R(wi/x) which itself in turn is defined in terms of a cost function lij. More specifically lij is the loss incurred for deciding wi when wj is the case. Now the associated expected loss when deciding wi is called the conditional risk and is given by

R (wi/x) - li1P(w1/x) + li2P(w2/x) i = 1, 2

The overall risk is a sum in the same way that the average probability of error was, R (wi/x) now playing the role of P(wi/x). The overall risk is minimised by

[R (w1/x) < R (w2/x) -> x is relevant, x is non-relevant] D2