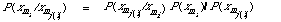an edge.) The resulting Pt(x) will be the same as can easily be shown by using the fact that

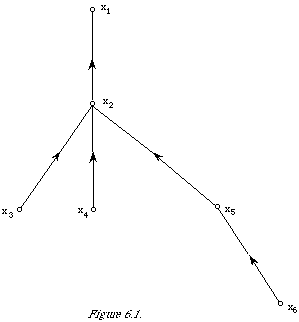
Applying this to the link between the root node x1 and its immediate descendant x2 in the example will shift the root to x2 and change the expansion to

Pt(x1, x2, ... x6) = P(x2)P(x1)/x2)P(x3/x2)P(x4/x2)P(x5/x2)P (x6/x5)

Of course, to satisfy the rule about relabelling we would exchange the names '1' and '2'. All expansions transformed in this way are equivalent in terms of goodness of approximation to P(x). It is therefore the tree which represents the class of equivalent expansions. Clearly there are a large number of possible dependence trees, the approximation problem we have is to find the best one; which amounts to finding the best permutation and mapping j(.).

In what follows I shall assume that the relabelling has been done and that xmi = xi.

Selecting the best dependence trees

Our problem now is to find a probability function of the formPt(x) on a set of documents which is the bestapproximation to the true joint