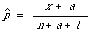|
|
126 |
|
|
|
|
In general we would have two tables of this kind when setting up our function g(x), one for estimating the parameters associated with P(x/w1) and one for P(x/w2).
In the limit we would have complete knowledge of which documents in the collection were relevant and which were not.
Were we to calculate the estimates for this limiting case, this would only be useful in showing what the upper bound to our retrieval would be under this particular model.
More realistically, we would have a sample of documents, probably small (not nesessarily random), for which the relevance status of each document was known.
This small set would then be the source data for any 2-by-2 tables we might wish to construct.
The estimates therefore would be biased in an unavoidable way.
The estimates shown above are examples of point estimates. There are a number of ways of arriving at an appropriate rule for point estimation. Unfortunately the best form of estimation rule is still an open problem[14]. In fact, some statisticians believe that point estimation should not be attempted at all[15]. However in the context of IR it is hard to see how one can avoid making point estimates. One major objection to any point estimation rule is that in deriving it some 'arbitrary' assumptions are made. Fortunately in IR there is some chance of justifying these assumptions by pointing to experimental data gathered from retrieval systems, thereby removing some of the arbitrariness.
Two basic assumptions made in deriving any estimation rule through Bayesian decision theory are: (1) the form of the prior distribution on the parameter space, i.e. in our case the assumed probability distribution on the possible values of the binomial parameter; and (2) the form of the loss function used to measure the error made in estimating the parameter.
Once these two assumptions are made explicit by defining the form of the distribution and loss function, then, together with Bayes' Principle which seeks to minimise the posterior conditional expected loss given the observations, we can derive a number of different estimation rules. The statistical literature is not much help when deciding which rule is to be preferred. For details the reader should consult van Rijsbergen[2] where further references to the statistical literature are given. The important rules of estimating a proportion p all come in the form
where x is the number of successes in n trials, anda and b are parameters dictated by the particularcombination of prior and loss |
|
|
126 |
|
|
|