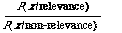|
|
128 |
|
|
|
|
objected to on the same grounds that one might object to the probability of Newton's Second Law of Motion being the case.
Some would argue that the probability is either one or zero depending on whether it is true or false.
Similarly one could argue for relevance.
The second point is that the probability P(relevance/document) can be got at by considering the inverse probability P(x/relevance), thus relating the two through Bayes' Theorem.
It is not that I am questioning the use of Bayes' Theorem when applied to probabilities, which is forced upon us anyhow if we want to use probability theory consistently, no, what I am questioning is that P(x/relevance) means something in IR and hence can lead us to P(relevance/x).
I think that we have to assume that it does, and realise that this assumption will enable us to connect P(relevance/x) with the distributional information about index terms.
To approach the problem in this way would be useless unless one believed that for many index terms the distribution over the relevant documents is different from that over the non-relevant documents. If we assumed the contrary, that is P(x/relevance) = P(x/non-relevance) then the P(relevance/document) would be the same as the prior probability of P(relevance), constant for all documents and hence incapable of discriminating them which is of no use in retrieval. So really we are assuming that there is indirect information available through the joint distribution of index terms over the two sets which will enable us to discriminate them. Once we have accepted this view of things then we are also committed to the formalism derived above. The commitment is that we must guess at P(relevance/document) as accurately as we can, or equivalently guess at P(document/relevance) and P(relevance), through the distributional knowledge we have of the attributes (e.g. index terms) of the document.
The elaboration in terms of ranking rather than just discrimination is trivial: the cut-off set by the constant in g(x) is gradually relaxed thereby increasing the number of documents retrieved (or assigned to the relevant category). The result that the ranking is optimal follows from the fact that at each cut-off value we minimise the overall risk. This optimality should be treated with some caution since it assumes that we have got the form of the P(x/wi)'s right and that our estimation rule is the best possible. Neither of these are likely to be realised in practice.
If one is prepared to let the user set the cut-off after retrieval has taken place then the need for a theory about cut-off disappears. The implication is that instead of working with the ratio
|
|
|
128 |
|
|
|