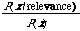In the latter case we do not see the retrieval problem as one of discriminating between relevant and non-relevant documents, instead we merely wish to compute the P(relevance/x) for each document x and present the user with documents in decreasing order of this probability. Whichever way we look at it we still require the estimation of two joint probability functions.

The decision rules derived above are couched in terms of P(x/wi). Therefore one would suppose that the estimation of these probabilities is crucial to the retrieval performance, and of course the fact that they can only be estimated is one explanation for the sub-optimality of the performance. To facilitate the estimation one makes assumptions about the form of P(x/wi). An obvious one is to assume stochastic independence for the components of x. But in general I think this is unrealistic because it is in the nature of information retrieval that index terms will be related to one another. To quote an early paper of Maron's on this point: 'To do this [enlarge upon a request] one would need to program a computing machine to make a statistical analysis of index terms so that the machine will "know" which terms are most closely associated with one another and can indicate the most probable direction in which a given request should be enlarged' [Maron's italics][4]. Therefore a more realistic approach is to assume some sort of dependence between the terms when estimating P(x/w1) and P(x/w2) (or P(x)).

I will now proceed to discuss ways of using this probabilistic model of retrieval and at the same time discuss some of the practical problems that arise. At first I will hardly modify the model at all. But then I will discuss a way of using it which does not necessarily accord strictly with the assumptions upon which it was built in the first place. Naturally the justification for any of this will lie in the province of experimental tests of which many still remain to be done[17]. But first I shall explain a minor modification arising from the need to reduce the dimensionality of our problem.

The curse of dimensionality

In deriving the decision rules I assumed that a document is represented by an n-dimensional vector where n is the size of the index term vocabulary. Typically n would be very large, and so the dimension of the(binary) document vectors is always likely to be greater than the