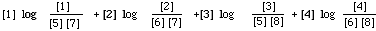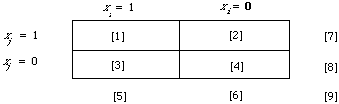
When computing I(xi,xj) for the purpose of constructing an MST we need only to know the rank ordering of the I(xi,xj)'s. The absolute values do not matter. Therefore if we use simple maximum likelihood estimates for the probabilities based on the data contained in the following table (using the same notation as on p.125).

then I(xi,xj) will be strictly monotone with

This is an extremely simple formulation of EMIM and easy to compute. Consider the case when it is P(x) we are trying to calculate. The MST is then based on co-occurrence data derived from the entire collection. Once we have this (i.e. [1]) and know the number of documents ([9]) in the file then any inverted file will contain the rest of the frequency data needed to fill in the counts in the other cells. That is from [5] and [7] given by the inverted file we can deduce [2] [3] [4] [6] and [8].

The problem of what to do with zero entries in one of the cells 1 to 4 is taken care of by letting 0 log 0 = 0. The marginals cannot be zero since we are only concerned with terms that occur at least once in the documents.

Next we discuss the possibility of approximation. Maron and Kuhns[19] in their early work used

d(xi,xj) = P(xi = 1, xj = 1) - P(xi =1) P(xj = 1) (*)

to measure the deviation from independence for any two index terms i and j. Apart from the log this is essentially the first term of the EMIM expansion. An MST (dependence tree) constructed on the basis of (*) clearlywould not lead to an optimal approximation ofP(x/wi) but the fit might be good enoughand certainly the corresponding tree can be