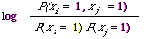as a measure of association. No doubt there are other ways of approximating the EMIM which are easier to compute, but whether they can be used to find a dependence tree leading to good approximation of the joint probability function must remain a matter for experimental test.

2. Calculation of MST

There are numerous published algorithms for generating an MST from pairwise association measures, the most efficient probably being the recent one due to Whitney[21]. The time dependence of his algorithm is 0(n^2) where n is the number of index terms to be fitted into the tree. This is not a barrier to its use on large data sets, for it is easy to partition the data by some coarse clustering technique as recommended on p.59, after which the total spanning tree can be generated by applying the MST algorithm to each cluster of index terms in turn. This will reduce the time dependence from 0(n^2) to 0(k^2) where k << n.

It is along these lines that Bentley and Friedman[22] have shown that by exploiting the geometry of the space in which the index terms are points the computation time for generating the MST can be shown to be almost always 0(n log n). Moreover if one is prepared to accept a spanning tree which is almost an MST then a computation time of 0(n log n) is guaranteed.

One major inefficiency in generating the MST is of course due to the fact that all n(n-1)/2 associations are computed whereas only a small number are in fact significant in the sense that they are non-zero and could therefore be chosen for a weight of an edge in the spanning tree. However, a high proportion are zero and could safely be omitted. Unfortunately, the only way we can ignore them is to first compute them. Croft[23] in a recent design for the single-link algorithm has discovered a way of ignoring associations without first computing them. It does however presuppose that a file and its inverted form are available, so that if this is not so some computation time would need to be invested in the inversion. It may be that a similar algorithm could be devised for computing anMST.