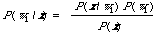It must be emphasised that in the non-linear case the estimation of the parameters for g(x) will ideally involve a different MST for each of P(x/w1) and P(x/w2). Of course one only has complete information about the distribution of index terms in the relevant/non-relevant sets in an experimental situation. The calculation of g(x) using complete information may be of interest when deriving upper bounds for retrieval effectiveness under the model as for example was done for the independent case in Robertson and Sparck Jones[1]. In an operational situation where no relevant documents are known in advance, the technique of relevance feedback would have to be used to estimate the parameters repeatedly so that the performance may converge to the upper bound. That in theory the convergence will take place is guaranteed by the convergence theorem for the linear case at least as discussed on p. 106 in Chapter 5. The limitations mentioned there also apply here.

There is a choice of how one would implement the model for g(x) depending on whether one is interested in setting the cut-off a prior or a posteriori. In the former case one is faced with trying to build an MST for the index terms occurring in the relevant documents and one for the ones occurring in the non-relevant documents. Since one must do this from sample information the dependence trees could be far from optimal. One heuristic way of meeting the situation is to construct a dependence tree for the whole collection. The structure of this tree is then assumed to be the structure for the two dependence trees based on the relevant and non-relevant documents. P(x/w1) and P(x/w2) are then calculated by computing the conditional probabilities for the connected nodes dictated by the one dependence tree. How good this particular approximation is can only be demonstrated by experimental test.

If one assumes that the cut-off is set a posteriori then we can rank the documents according to P(w1/x) and leave the user to decide when he has seen enough. In other words we use the form

to calculate (estimate) the probability of relevance for each document x. Now here we only need to estimate for P(x/w1), since top calculate P(x) we simply use the spanning tree for the entire collection without considering relevance information at all. This second approach has some advantages (ignoring the absence of anexplicit mention of cut-off), one being that if dependence is assumedon the entire collection then this is consistent with assumingindependence on the relevant documents,