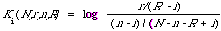The way we interpret this hypothesis is that a term in the query used by a user is likely to be there because it is a good discriminator and hence we are interested in its close associates. The hypothesis does not specify the way in which association between index terms is to be measured although in this chapter I have made a case for using EMIM. Neither does it specify a measure of 'discrimination', this I consider in the next section. The Association Hypothesis in some ways is a dual to the Cluster Hypothesis (p. 45) and can be tested in the same way.

Discrimination power of an index term

On p. 120 I defined

and in fact there made the comment that it was a measure of the power of term i to discriminate between relevant and non-relevant documents. The weights in the weighting function derived from the independence assumption A1 are exactly these Ki's. Now if we forget for the moment that these weights are a consequence of a particular model and instead consider the notion of discrimination power of an index term on its own merits. Certainly this is not a novel thing to do, Salton in some of his work has sought effective ways of measuring the 'discrimination value' of index terms[24]. It seems reasonable to attach to any index term that enters into the retrieval process a weight related to its discrimination power. Ki as a measure of this power is slightly awkward in that it becomes undefined when the argument of the log function becomes zero. We therefore seek a more 'robust' function for measuring discrimination power. The function I am about to recommend for this purpose is indeed more robust, has an interesting interpretation, and enables me to derive a general result of considerable interest in the next section. However, it must be emphasised that it is only an example of a function which enables some sense to be make of the notion 'discrimination power' in this and the next section. It should therefore not be considered unique although it is my opinion that any alternative way of measuring discrimination power in this context would come very close to the measure I suggest here.

Instead of Ki I suggest using the information radius, defined in Chapter 3 on p. 42, as a measure of the discrimination power of an index term. It is a close cousin of the expected mutual information measure a relationship that will come in useful later on. Using u and v as positive weights such as u +v = 1 and the usual notation for the