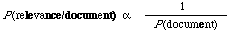According to Doyle[32] (p.267), Maron and Kuhns[19] were the first to describe in the open literature the use of association (statistical co-occurrence) of index terms as a means of enlarging and sharpening the search. However, Doyle himself was already working on similar ideas in the late fifties[33] and produced a number of papers on 'associations' in the early sixties[34,35]. Stiles in 1961[36], already apparently aware of Maron and Kuhns work, gave an explicit procedure for using terms co-occurring significantly with search terms, and not unlike the method based on the dependence tree described in this chapter. He also used the [[chi]]^2 to measure association between index terms which is mathematically very similar to using the expected mutual information measure, although the latter is to be preferred when measuring dependence (see Goodman and Kruskal for a discussion on this point[37]). Stiles was very clear about the usefulness of using associations between index terms, he saw that through them one was 'able to locate documents relevant to a request even though the document had not been indexed by the term used in the request'[36].

The model in this chapter also connects with two other ideas in earlier research. One is the idea of inverse document frequency weighting already discussed in Chapter 2. The other is the idea of term clustering. Taking the weighting idea first, this in fact goes back to the early paper by Edmundson and Wyllys[38], we can write

or in words, for any document the probability of relevance is inversely proportional the probability with which it will occur on a random basis. If the P(document) is assumed to be the product of the probabilities of the individual index terms being either present or absent in the document then after taking logs we have the inverse document frequency weighting principle. It assumes that the likelihood P(document/relevance) is constant for all documents. Why it is exactly