I must emphasise that the above argument leading to the hypothesis is not a proof. The argument is only a qualitative one although I believe it could be tightened up. Despite this it provides (together with the hypothesis) some justification and theoretical basis for the use of the MST based on I (xi, xj) to improve retrieval. The discrimination hypothesis is a way of firming up the Association Hypothesis under conditional independence.

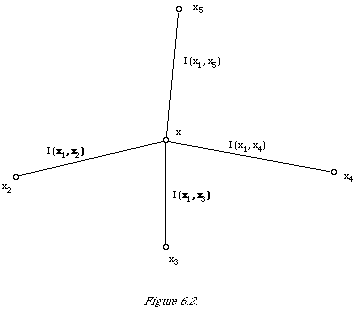
One consequence of the discrimination hypothesis is that it provides a rationale for ranking the index terms connected to a query term in the dependence tree in order of I(term, query term) values to reflect the order of discrimination power values. The basis for this is that the more strongly connected an index term is to the query term (measured by EMIM) the more discriminatory it is likely to be. To see what is involved more clearly I have shown an example set-up in Figure 6.2. Let us suppose that x1 is the variable corresponding to the query term and that I (x1, x2) < I (x1, x3) < I (x1, x4) < I (x1, x5) then our hypothesis says that without knowing in advance how good a discriminator each of the index terms 2,3,4,5 is, it is reasonable to assume that I (x2, W) < I (x3, W) < I (x4, W) <I (x5, W). Clearly we cannot guarantee that the index terms will satisfy the last ordering but it is the best we can do given our ignorance.

Bibliographic remarks

The basis background reading for this chapter is contained in but a few papers. One approach to probabilistic weighting based on relevance data