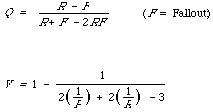Composite measures

Dissatisfaction in the past with methods of measuring effectiveness by a pair of numbers (e.g. precision and recall) which may co-vary in a loosely specified way has led to attempts to invest composite measures. These are still based on the 'contingency' table but combine parts of it into a single number measure. Unfortunately many of these measures are rather ad hoc and cannot be justified in any rational way. The simplest example of this kind of measure is the sum of precision and recall

S = P + R

This is simply related to a measure suggested by Borko

BK = P + R - 1

More complicated ones are

Vickery's measure V can be shown to be a special case of a general measure which will be derived below.

Some single-number measures have derivations which can be justified in a rational manner. Some of them will be given individual attention later on. Suffice it here to point out that it is the model underlying the derivation of these measures that is important.

The Swets model*

As early as 1963 Swets[12] expressed dissatisfaction with existing methods of measuring retrieval effectiveness. His background in signal detection led him to formulate an evaluation model based on statistical decision theory. In 1967 he evaluated some fifty different retrieval methods from the point of view of his model[13]. The results of his evaluation were encouraging but not conclusive. Subsequently, Brookes[14] suggested some reasonable modifications to Swets' measure of effectiveness, and Robertson[15] showed that the suggested modifications were in fact simply related to an alternative measure already suggested by Swets. * Bookstein[16] has recently re-examined this model showing how Swets implicitly relied on an 'equal variance' assumption.

It is interesting that although the Swets model is theoreticallyattractive