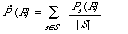Gs = (R[[theta]]s, P[[theta]]s )

the set of observed points for a request. To interpolate between any two points we define:

Ps(R) = {sup P : R' >= R s.t. (R', P) [[propersubset]] Gs}

where R is a standard recall value. From this we obtain the average precision value at the standard recall value R by:

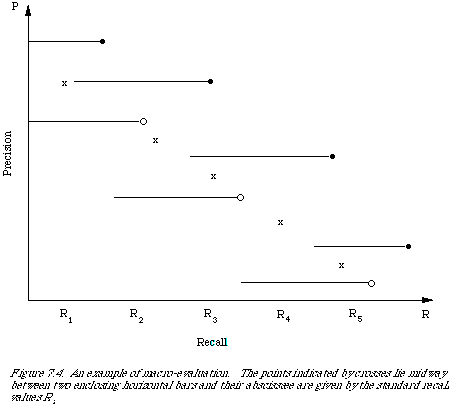
The set of observed points is such that the interpolated function is monotonically decreasing. Figure 7.3 shows the effect of the interpolation procedure, essentially it turns the P-R curve into a step-function with the jumps at the observed points. A necessary consequence of its monotonicity is that the average P-R curve will also be monotonically decreasing. It is possible to define the set of observed points in such a way that the interpolate function is not monotonically decreasing. In practice, even for this case, we have that the average precision-recall curve is monotonically decreasing.

In Figure 7.4 we illustrate the interpolation and averaging process.