He accepts the validity of measuring the effectiveness of retrieval by a curve either precision-recall or recall-fallout generated by the variation of some control variable [[lambda]] (e.g. co-ordination level). He seeks to characterise each curve by a single number. He rejects precision-recall in favour of recall-fallout since he is unable to do it for the former but achieves limited success with the latter.

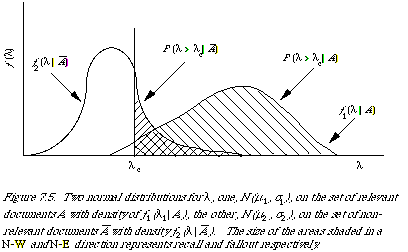
In the simplest case we assume that the variable [[lambda]] is distributed normally on the set of relevant and non-relevant documents. The two distributions are given respectively by N(u1, [[sigma]]1) and N(u2, [[sigma]]2). The density functions are given by [[florin]]1 ([[lambda]]|A) and [[florin]]2 ([[lambda]]|`A). We may picture the distribution as shown in Figure 7.5.

The usual set-up in IR is now to define a decision rule in terms of [[lambda]], to determine which documents are retrieved (the acceptance criterion). In other words we specify [[lambda]]c such that a document for which the associated [[lambda]] exceeds [[lambda]]c is retrieved. We now measure the effectiveness of a retrieval strategy by measuring some appropriate variables (such as R and P, or R and F) at various values of [[lambda]]c. It turns out that the differently shaded areas under the curves in Figure 7.5 correspond to recall and fallout. Moreover, we find the operating characteristic (OC) traced outby the point (F[[lambda]], R[[lambda]]) due to variationin [[lambda]]c is a smooth curve fully determined by two points, inthe general case of unequal variance, and