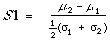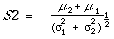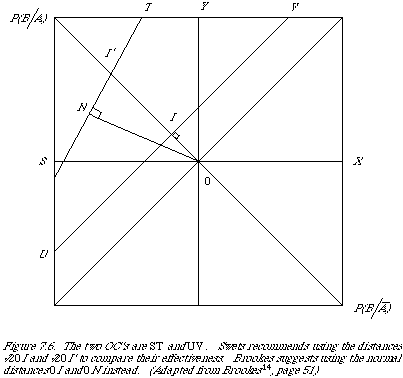
by one point in the special case of equal variance. To see this one only needs to plot the (F[[lambda]], R[[lambda]]) points on double probability paper (scaled linearly for the normal deviate) to find that the points lie on a straight line. A slope of 45deg. corresponds to equal variance, and otherwise the slope is given by the ratio of [[sigma]]1 and [[sigma]]2. Figure 7.6 shows the two cases. Swets now suggests, regardless of

slope, that the distance 0I (actually [[radical]]20I) be used as a measure of effectiveness. This amounts to using:

which is simply the difference between the means of the distribution normalised by the average standard deviation. Unfortunately this measure does rather hide the fact that a high S1 value may be due to a steep slope. The slope, and S1, would have to be given which fails to meet Swets' second condition. We, also, still have the problem of deciding between two strategies whose OC's intersect and hence have different S1 values and slopes.

Brookes[14] in an attempt to correct for the S1 bias towards systems with slopes much greater than unity suggested a modification to S1. Mathematically Brookes's measure is