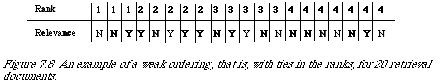Unfortunately the ranking generated by a matching function is rarely a simple ordering, but more commonly a weak ordering. This means that at any given level in the ranking, there is at l;east one document (probably more) which makes the search length inappropriate since the order of documents within a level is random. If the information need is met at a certain level in the ordering then depending on the arrangement of the relevant documents within that level we shall get different search lengths. Nevertheless we can use an analogous quantity which is the expected search length. For this we need to calculate the probability of each possible search length by juggling (mentally) the relevant and non-relevant documents in the level at which the user need is met.

For example, consider the weak ordering in Figure 7.8. If the query is of Type 2 with n = 6 then the need is met at level 3. The possible search lengths are 3, 4, 5 or 6

depending on how many non-relevant documents precede the sixth relevant document. We can ignore the possible arrangements within levels 1 and 2; their contributions are always the same. To compute the expected search length we need the probability of each possible search length. We get at this by considering first the number of different ways in which two relevant documents could be distributed among five, it is ([5]2) = 10. Of these 4 would result in a search length of 3, 3 in a search length of 4, 2 in a search length of 5 and 1 in a search length of 6. Their corresponding probabilities are therefore, 4/10, 3/10, 2/10 and 1/10. The expected search length is now:

(4/10) . 3 + (3/10) . 4 + (2/10) . 5 + (1/10) . 6 = 4

The above procedure leads immediately to a convenient 'intuitive' derivation of a formula for the expected search length. It seems plausible that the average results of many randomsearches through the final level (level at which need is met) will bethe same as for a single