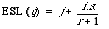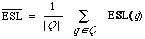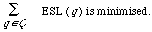(a) q is the query of given type;

(b) j is the total number of documents non-relevant to q in all levels preceding the final;

(c) r is the number of relevant documents in the final level;

(d) i is the number of non-relevant documents in the final level;

(e) s is the number of relevant documents required from the final level to satisfy the need according its type.

Now, to distribute the r relevant documents evenly among the non-relevant documents, we partition the non-relevant documents into r + 1 subsets each containing i /(r + 1) documents. The expected search length is now:

As a measure of effectiveness ESL is sufficient if the document collection and test queries are fixed. In that case the overall measure is the mean expected search length

where Q is the set of queries. This statistic is chosen in preference to any other for the property that it is minimised when the total expected search length

To extend the applicability of the measure to deal with varying test queries and document collections, we need to normalise the ESL in some way to counter the bias introduced because:

(1) queries are satisfied by different numbers of documents according to the type of the query and therefore can be expected to have widely differing search lengths;

(2) the density of relevant documents for a query in one document collection may be significantly different from the density in another.

The first item suggests that the ESL per desired relevant document is really what is wanted as an index of merit. The second suggests