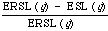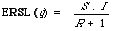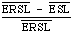|
|
163 |
|
|
|
|
normalising the ESL by a factor proportional to the expected number of non-relevant documents collected for each relevant one.
Luckily it turns out that the correction for variation in test queries and for variation in document collection can be made by comparing the ESL with the expected random search length (ERSL).
This latter quantity can be arrived at by calculating the expected search length when the entire document collection is retrieved at one level.
The final measure is therefore:
which has been called the expected search length reduction factor by Cooper. Roughly it measures improvement over random retrieval. The explicit form for ERSL is given by:
where
(1) R is the total number of documents in the collection relevant to q; (2) I is the total number of documents in the collection non-relevant to q; (3) S is the total desired number of documents relevant to q.
The explicit form for ESL was given before. Finally, the overall measure for a set of queries Q is defined, consistent with the mean ESL, to be
which is known as the mean expected search length reduction factor.
Within the framework as stated at the head of this section this final measure meets the bill admirably. However, its acceptability as a measure of effectiveness is still debatable (see, for example, Senko[21]). It totally ignores the recall aspect of retrieval, unless queries are evaluated which express the need for a certain proportion of the relevant documents in the system. It therefore seems to be a good substitute for precision, one which takes into account order of retrieval and user need.
For a further defence of its subjective nature see Cooper[1]. A spirited attack on Cooper's position can be found in Soergel[22].
|
|
|
163 |
|
|
|