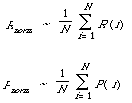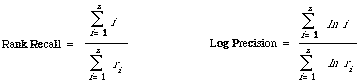|
|
166 |
|
|
|
|
differ considerably from those which the user feels are pertinent (Senko[21]).
Or, as Salton[23] (page 289) puts it: 'the normalised precision measure assigns a much larger weight to the initial (low) document ranks than to the later ones, whereas the normalised recall measure assigns a uniform weight to all relevant documents'.
Unfortunately, the weighting is arbitrary and given.
Thirdly, it can be shown that normalised recall and precision have interpretations as approximations to the average recall and precision values for all possible cut-off levels.
That is, if R (i) is the recall at rank position i, and P (i) the corresponding precision value, then:
Fourthly, whereas Cooper has gone to some trouble to take account of the random element introduced by ties in the matching function, it is largely ignored in the derivation of Pnorm and Rnorm.
One further comment of interest is that Robertson15 has shown that normalised recall has an interpretation as the area under the Recall-Fallout curve used by Swets.
Finally mention should be made of two similar but simpler measures used by the SMART system. They are:
and do not take into account the collection size N, n is here the number of relevant documents for the particular test query.
A normalised symmetric difference
Let us now return to basics and consider how it is that users could simply measure retrieval effectiveness. We are considering the common situation where a set of documents isretrieved in response to a query, |
|
|
166 |
|
|
|