|
|
173 |
|
|
|
|
It will turn out that the F which is appropriate can be simply transformed into an additive representation.
The transformation is f (F) = - (F - 1)[-1] which is strictly monotonically increasing in the range 0 <= F <= 1, which is the range of interest.
In any case, when measuring retrieval effectiveness any strictly monotone transformation of the measure will do just as well.
Explicit measures of effectiveness
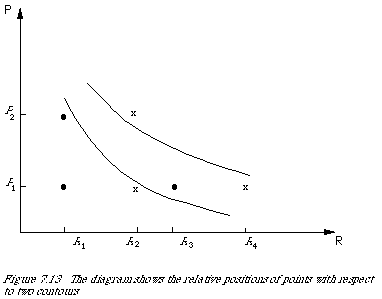
I shall now argue for a specific form of [[Phi]]i and F, based on a model for the user. In other words, the form [[Phi]]i and F are partly determined by the user. We start by showing how the ordering on R x P in fact induces an ordering of intervals on each factor. From Figure 7.13 we have that (R3, P1) >= (R1, P2), (R3, P1) >= (R1, P1) and (R1, P2) >= (R1, P1). Therefore the increment (interval) R1R3 is preferred to the increment P1P2. But (R2, P2) >= (R4, P1), which gives P1 P2 is preferred to R2 R4. Hence R1 R3 >=1 R2, R4 where >=1 is the induced order relation on R. We now have a method of comparing each interval on R with a fixed interval on P.
Since we have assumed that effectiveness is determined by precision and recall we have committed ourselves to the importance of proportions of documents rather than absolute numbers.
Consistent with this is the assumption of decreasing marginal effectiveness.
Let me illustrate this with an example.
Suppose the user is willing to sacrifice
|
|
|
173 |
|
|
|