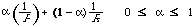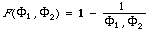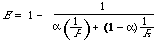(R + 1, P - 1) > (R, P)

but

(R + 1, P) > (R + 2, P - 1)

We conclude that the interval between R + 1 and R exceeds the interval between P and P - 1 whereas the interval between R + 1 and R + 2 is smaller. Hence the marginal effectiveness of recall is decreasing. (A similar argument can be given for precision.) The implication of this for the shape of the curves of equal effectiveness is that they are convex towards the origin.

Finally, we incorporate into our measurement procedure the fact that users may attach different relative importance to precision and recall. What we want is therefore a parameter (ß) to characterise the measurement function in such a way that we can say: it measures the effectiveness of retrieval with respect to a user who attaches ß times as much importance to recall as precision. The simplest way I know of quantifying this is to specify the P/R ratio at which the user is willing to trade an increment in precision for an equal loss in recall.

Definition 6. The relative importance a user attaches to precision and recall is the P/R ratio at which [[partialdiff]]E/ [[partialdiff]]R = [[partialdiff]]E/ [[partialdiff]]P, where E = E(P, R) is the measure of effectiveness based on precision and recall.

Can we find a function satisfying all these conditions? If so, can we also interpret it in an intuitively simple way? The answer to both these questions is yes. It involves:

The scale functions are therefore, [[Phi]]1(P) = [[alpha]](1/P), and [[Phi]]2(R) = (1 - [[alpha]]) (1/R). The 'combination' function F is now chosen to satisfy definition 6 without violating the additive independence. We get:

We now have the effectiveness measure. In terms of P and R it will be: