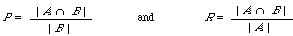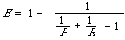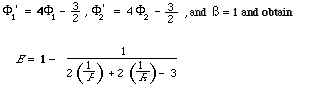To facilitate interpretation of the function, we transform according to [[alpha]] = 1/(ß^2 + 1), and find that [[partialdiff]]E/ [[partialdiff]]R = [[partialdiff]]E/ [[partialdiff]]P when P/R = ß. If A is the set of relevant documents and B the set of retrieval documents, then:

E now gives rise to the following special cases:

(1) When [[alpha]] = 1/2 (ß = 1) E = |A [[Delta]] B | / (|A | + |B |), a normalised symmetric difference between sets A and B (A [[Delta]] B = A [[union]] B - A [[intersection]] B). It corresponds to a user who attaches equal importance to precision and recall.

(2) E -> 1 - R when [[alpha]] -> 0 (ß -> *), which corresponds to a user who attaches no important to precision.

(3) E -> 1 - P when [[alpha]] -> 1 (ß -> 0), which corresponds to a user who attaches no importance to recall.

It is now a simple matter to show that certain other measures given in the literature are special cases of the general form E. By the representation theorem, the [[Phi]]i 's are uniquely determined up to a linear transformation, that is, [[Phi]]i['] = [[Theta]][[Phi]]i + [[gamma]]i would serve equally well as scale functions. If we now set [[Phi]]1['] = 2[[Phi]]1 - 1/2, [[Phi]]2['] = 2[[Phi]]2 - 1/2, and ß = 1 then we have:

which is the measure recommended by Heine[3].

One final example is the measure suggested by Vickery in 1965 which was documented by Cleverdon et al.[27]. Here we set:

which is Vickery's measure (apart from a scale factor of 100).

To summarise, we have shown that it is reasonable to assume thateffectiveness in terms of precision and recall determines an additive