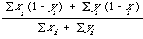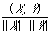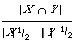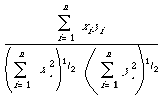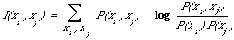where summation is over the total number of different keywords in the document collection.

Salton considered document representatives as binary vectors embedded in an n-dimensional Euclidean space, where n is the total number of index terms.

can then be interpreted as the cosine of the angular separation of the two binary vectors X and Y. This readily generalises to the case where X and Y are arbitrary real vectors (i.e. weighted keyword lists) in which case we write

where (X, Y) is the inner product and || . || the length of a vector. If the space is Euclidean then for

X = (x1, ..., xn) and Y = (y1, ..., yn)

we get

Some authors have attempted to base a measure of association on a probabilistic model[18]. They measure the association between two objects by the extent to which their distributions deviate from stochastic independence. This way of measuring association will be of particular importance when in Chapter 5 I discuss how the association between index terms is to be used to improve retrieval effectiveness. There I use the expected mutual information measure to measure association. For two discrete probability distributions P(xi) and P(xj) it can be defined as follows:

When xi and xj are independent P(xi)P(xj) = P(xi,xj) and so I(xi,xj) = 0. Also I(xixj) = 0. Also I(xixj) = I(xjxi) which shows that it is symmetric. It also has the