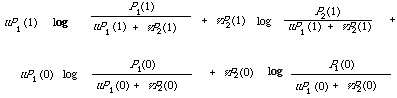|
|
42 |
|
|
|
|
nice property of being invariant under one-to-one transformations of the co-ordinates.
Other interesting properties of this measure may be found in Osteyee and Good[19].
Rajski[20] shows how I(xixj) may be simply transformed into a distance function on discrete probability distributions.
I(xixj) is often interpreted as a measure of the statistical information contained in xi about xj (or vice versa).
When we apply this function to measure the association between two index terms, say i and j, then xi and xj are binary variables.
Thus P(xi = 1) will be the probability of occurrence of the term i and similarly P(xi = 0) will be the probability of its non-occurrence.
The extent to which two index terms i and j are associated is then measured by I(xixj) which measures the extent to which their distributions deviate from stochastic independence.
A function very similar to the expected mutual information measure was suggested by Jardine and Sibson[2] specifically to measure dissimilarity between two classes of objects. For example, we may be able to discriminate two classes on the basis of their probability distributions over a simple two-point space {1, 0}. Thus let P1(1), P1(0) and P2(1), P2(0) be the probability distributions associated with class I and II respectively. Now on the basis of the difference between them we measure the dissimilarity between I and II by what Jardine and Sibson call the Information Radius, which is
Here u and v are positive weights adding to unit. This function is readly generalised to multi-state, or indeed continuous distribution. It is also easy to shown that under some interpretation the expected mutual information measure is a special case of the information radius. This fact will be of some importance in Chapter 6. To see it we write P1(.) and P2(.) as two conditional distributions P(./w1) and P(./w2). If we now interpret u = P(./w1) and v = P(./w2), that is the prior probability of the conditioning variable in P(./wi), then on substituting into the expression for the information radius and using the identities.
P(x) = P(x/w1) P(w1) + P(x/w2) P(w2) x = 0, 1
P(x/wi) = P(x/wi) P(x) i = 1, 2
we recover the expected mutual information measure I(x,wi).
|
|
|
42 |
|
|
|