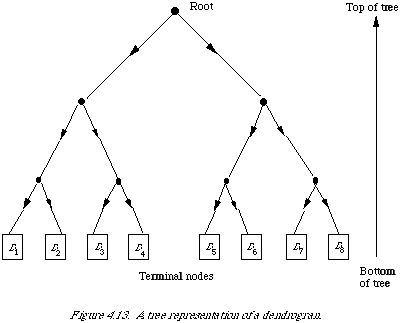
By now it is perhaps apparent that when we were talking about ring structures and threaded lists in some of our examples we were really demonstrating how to implement a tree structure. The dendrogram in Figure 4.7 can easily be represented as a tree (Figure 4.13). The documents are stored at the terminal nodes and each node represents a class (cluster) of documents. A search for a particular set of documents would be initiated at the root and would proceed along the arrows until the required class was found.

Another example of a tree structure is the directory associated with an index-sequential file. It was described as a hierarchy of indexes, but could equally well have been described as a tree structure.

The use of tree structures in computer science dates back to the early 1950s when it was realised that the so-called binary search could readily be represented by a binary tree. A binary tree is one in which each node (except the terminal nodes) has exactly two branches leaving it. A binary search is an efficient method for detecting the presence or absence of a key value among a set of keys. It presupposes that the keys have been sorted. It proceeds by successive division of the set, at each division discarding half the current set as not containing the sought key. When the set contains N sorted keys the search time is of order log2N. Furthermore, after some thought one can see how this process can be simply represented by a binary tree.