Unfortunately, in many applications one wants the ability to insert a key which has been found to be absent. If the keys are stored sequentially then the time taken by the insertion operation may be of order N. If one, however, stores the keys in a binary tree this lengthy insert time may be overcome, both search and insert time will be of order log2N. The keys are stored at the nodes, at each node a left branch will lead to 'smaller' keys, a right branch will lead to 'greater' keys. A search terminating on a terminal node will indicate that the key is not present and will need to be inserted.

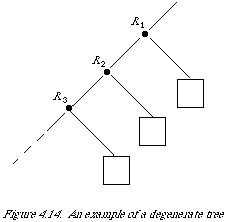
The structure of the tree as it grows is largely dependent on the order in which new keys are presented. Search time may become unnecessarily long because of the lop-sidedness of the tree. Fortunately, it can be shown (Knuth[28]) that random insertions do not change the expected log2N time dependence of the tree search. Nevertheless, methods are available to prevent the possibility of degenerate trees. These are trees in which the keys are stored in such a way that the expected search time is far from optimal. For example, if the keys were to arrive for insertion already ordered then the tree to be built would simply be as shown in Figure 4.14.

It would take us too far afield for me to explain the techniques for avoiding degenerate trees. Essentially, the binary tree is maintained in such a way that at any node the subtree on the left branch has approximately as many levels as the subtree on the right branch. Hence the name balanced tree for such a tree. The search paths in a balanced tree will never be more than 45 per cent longer than the optimum. The expected search and insert times are still of order log N. For further details the reader is recommended to consult Knuth[28].