|
|
96 |
|
|
|
|
for the query.
This formulation only makes sense if the queries are
expressed in terms of index terms (or keywords) and combined by the
usual logical connectives AND, OR, and NOT.
For example, if the query
Q = (K1 AND K2) OR (K3 AND (NOT
K4)) then the Boolean search will retrieve all documents
indexed by K1 and K2, as well as all documents indexed
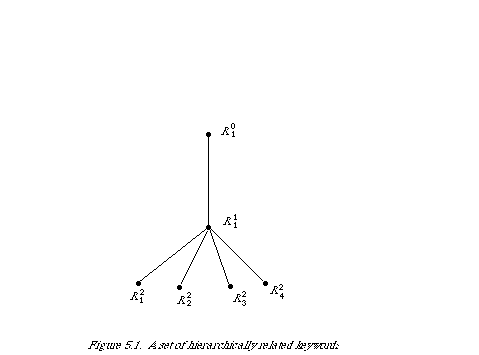
by K3 which are not indexed by K4. Some systems which operate by means of Boolean searches allow the user to narrow or broaden the search by giving the user access to a structured dictionary which for any given keyword stores related keywords whichmay be more general or more precise. For example, in the tree structure in Figure 5.1, the keyword K^1_1 is contained in the more general keyword K^0_1, but it can also be split up into 4 more precise keywords K^2_1, K^2_2, K^2_3, and K^2_4. Therefore, if one has an interactive system the search can easily be reformulated using some of these related terms.
An obvious way to implement the Boolean search is through the inverted file. We store a list for each keyword in the vocabulary, and in each list put the addresses (or numbers) of the documents containing that particular word. To satisfy a query we now perform the set operations, corresponding to the logical connectives, on the Ki-lists. For example, if
K1 -list : D1, D2, D3, D4 K2 -list : D1, D2 K3 -list : D1, D2, D3 K4 -list : D1 and Q = (K1 AND K2) OR (K3 AND (NOT K4))
|
|
|
96 |
|
|
|