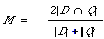|
|
97 |
|
|
|
|
then to satisfy the (K1 AND K2) part we intersect the K1 and K2 lists, to satisfy the (K3 AND (NOT K4)) part we subtract the K4 list from the K3 list.
The OR is satisfied by now taking the union of the two sets of documents obtained for the parts.
The result is the set {D1, D2, D3} which satisfies the query and each document in it is 'true' for the query.
A slight modification of the full Boolean search is one which only allows AND logic but takes account of the actual number of terms the query has in common with a document. This number has become known as the co-ordination level. The search strategy is often called simple matching. Because at any level we can have more than one document, the documents are said to be partially ranked by the co-ordination levels.
For the same example as before with the query Q = K1 AND K2 AND K3 we obtain the following ranking:
Co-ordination level 3 D1, D2 2 D3 1 D4
In fact, simple matching may be viewed as using a primitive matching function. For each document D we calculate |D [[intersection]] Q|, that is the size of the overlap between D and Q, each represented as a set of keywords. This is the simple matching coefficient mentioned in Chapter 3.
Matching functions
Many of the more sophisticated search strategies are implemented by means of a matching function. This is a function similar to an association measure, but differing in that a matching function measures the association between a query and a document or cluster profile, whereas an association measure is applied to objects of the same king. Mathematically the two functions have the same properties; they only differ in their interpretations.
There are many examples of matching functions in the literature. Perhaps the simplest is the one associated with the simple matching search strategy.
If M is the matching function, D the set of keywords representing the document, and Q the set representing the query, then:
|
|
|
97 |
|
|
|