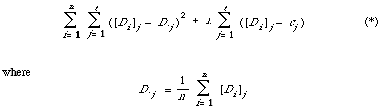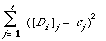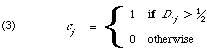This can be rewritten as

The expression (*) will be minimised, thus maximising the number of correct predictions, when C = (c1, . . . , ct) is chosen in such a way that

is a minimum. This is achieved by

So in other words a keyword will be assigned to a cluster representative if it occurs in more than half the member documents. This treats errors of prediction caused by absence or presence of keywords on an equal basis. Croft[7] has shown that it is more reasonable to differentiate the two types of error in IR applications. He showed that to predict falsely 0 (cj = 0) is more costly than to predict falsely a 1 (cj = 1). Under this assumption the value of [1]/2 appearing is (3) is replaced by a constant less than [1]/2, its exact value being related to the relative importance attached to the two types of prediction error.

Although the main reason for constructing these cluster representatives is to lead a search strategy to relevant documents, it should be clear that they can also be used to guide a search to documents meeting some condition on the matching function. For example, we may want to retrieve all documents Di which match Q better than T, i.e.

{Di |M (Q, Di) > T}

For more details about the evaluation of cluster representative (3) for this purpose the reader should consult the work of Yu et al. [8,9].

One major objection to most work on cluster representatives is that it treats the distribution of keywords in clusters as independent. This is not very realistic. Unfortunately, there does not appear to be any work to remedy the situation except that of Ardnaudov and Govorun[10].

Finally, it should be noted that cluster methods which proceed directly from document descriptions to the classification without first