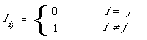[P( x/w1) P (w1) > P( x/w2) P(w2) -> x is relevant, x is non-relevant] D3

Notice that P(x) has disappeared from the equation since it does not affect the outcome of the decision. Now, using the definition R (wi/x) it is easy to show that

[R (w1/x) < R (w2/x) ] [[equivalence]] [(l21 - l11) P( x/w1) P(w1) > (l12 - l22) P( x/w2) P(w2)]

When a special loss function is chosen, namely,

which implies that no loss is assigned to a correct decision (quite reasonable) and unit loss to any error (not so reasonable), then we have

[R (w1/x) < R (w2/x) [[equivalence]] P(x/w1) P (w1) > P(x/w2) P(w2)]

which shows the equivalence of D2 and D3, and hence of D1 and D2 under a binary loss function.

This completes the derivation of the decision rule to be used to decide relevance or non-relevance, or to put it differently to retrieve or not to retrieve. So far no constraints have been put on the form of P(x/w1), therefore the decision rule is quite general. I have set up the problem as one of deciding between two classes thereby ignoring the problem of ranking for the moment. One reason for this is that the analysis is simpler, the other is that I want the analysis to say as much as possible about the cut-off value. When ranking, the cut-off value is usually left to the user; within the model so far one can still rank, but the cut-off value will have an interpretation in terms of prior probabilities and cost functions. The optimality of the probability ranking principle follows immediately from the optimality of the decision rule at any cut-off. I shall now go on to be more precise about the exact form of the probability functions in the decision rule.

Form of retrieval function

The previous section was rather abstract and left the connection of the various probabilities with IR rather open. although it is reasonable for us to want to calculateP(relevance/document) it is not at all clear as to how thisshould be done or whether the inversion through Bayes'