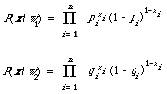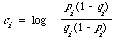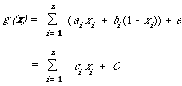|
|
118 |
|
|
|
|
Theorem is the best way of getting at it.
Nevertheless, we will proceed assuming that P(x/wi) is the appropriate function to estimate.
This function is of course a joint probability function and the interaction between the components of x may be arbitrarily complex.
To derive a workable decision rule a simplifying assumption about P(x/wi) will have to be made.
The conventional mathematically convenient way of simplifying P(x/wi) is to assume the component variables xi of x to be stochastically independent.
Technically this amounts to making the major assumption
P(x/wi) = P(x1/wi) P(x2/wi) ... P(xn/wi) A1
Later I shall show how this stringent assumption may be relaxed. We also for the moment ignore the fact that assuming independence conditional on both w1 and w2 separately has implications about the dependence conditional on w1 [[logicalor]] w2.
Let us now take the simplified form of P(x/wi) and work out what the decision rule will look like. First we define some variables
pi = Prob (xi = 1/w1) qi = Prob (xi = 1/w2).
In words pi(qi) is the probability that if the document is relevant (non-relevant) that the ith index term will be present. The corresponding probabilities for absence are calculated by subtracting from 1, i.e. 1 - pi = Prob (xi = 0/w1). The likelihood functions which enter into D3 will now look as follows
To appreciate how these expressions work, the reader should check that P((0,1,1,0,0,1)/w1) = (1 - p1)p2p3(1 - p4)(1 - p5)p6. Substituting for P(x/wi) in D3 and taking logs, the decision rule will be transformed into a linear discriminant function.
where the constants ai, bi and e are obvious.
|
|
|
118 |
|
|
|