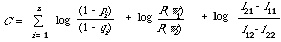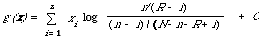and

The importance of writing it this way, apart from its simplicity, is that for each document x to calculate g(x) we simply add the coefficients ci for those index terms that are present, i.e. for those ci for which xi = 1. The ci are often looked up as weights; Robertson and Sparck Jones[1] call ci a relevance weight, and Salton calls exp(ci) the term relevance. I shall simply refer to it as a coefficient or a weight. Hence the name weighting function for g(x).

The constant C which has been assumed the same for all documents x will of course vary from query to query, but it can be interpreted as the cut-off applied to the retrieval function. The only part that can be varied with respect to a given query is the cost function, and it is this variation which will allow us to retrieve more or less documents. To see this let us assume that l11 = l22 = 0 and that we have some choice in setting the ratio l21/l11 by picking a value for the relative importance we attach to missing a relevant document compared with retrieving a non-relevant one. In this way we can generate a ranking, each rank position corresponding to a different ratio l21/l12.

Let us now turn to the other part of g(x), namely ci and let us try and interpret it in terms of the conventional 'contingency' table.

There will be one such table for each index term; I have shown it for the index term i although the subscript i has not been used in the cells. If we have complete information about the relevant and non-relevant documents in the collection then we can estimate pi by r/R and qi by (n - r)/(N - R). Therefore g(x) can be rewritten as follows:

This is in fact the weighting formula F4 used by Robertson and Sparck Jones1 in their so called retrospective experiments. For later