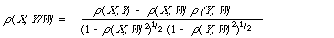|
|
137 |
|
|
|
|
the different contributions made to the measure by the different cells.
So, for example, an index term might be a good discriminator because it occurs frequently in the non-relevant documents and infrequently in the relevant documents.
Therefore, to weight an index term proportional to the discrimination measure whenever it is present in a document is exactly the wrong thing to do.
It follows that the data contained in the contingency table must be used when deciding on a weighting scheme.
Discrimination gain hypothesis
In the derivation above I have made the assumption of independence or dependence in a straightforward way. I have assumed either independence on both w1 and w2, or dependence. But, as implied earlier, this is not the only way of making these assumptions. Robertson and Sparck Jones[1] make the point that assuming independence on the relevant and non-relevant documents can imply dependence on the total set of documents. To see this consider two index terms i and j, and
P(xi, xj) = P(xi, xj /w1)P(w1) + P(xi, xi /w2) P (w2)
P(xi) P( xj) = [P(xi /w1)P(w1) + P(xi, w2) P (w2)] [P(xj /w1) P(w1) + P(xj,w2) P (w2)]
If we assume conditional independence on both w1 and w2 then
P(xi, xj) = P(xi, /w1) P(xj, w1) P(w1) + P(xi /w2) P(xj/ w2) P (w2)
For unconditional independence as well, we must have
P(xi, xj) = P(xi) P(xj)
This will only happen when P(w1) = 0 or P(w2) = 0, or P(xi/ w1) = P(xi/w2), or P(xj/w1) = P(xj /w2), or in words, when at least one of the index terms is useless at discriminating relevant from non-relevant documents. In general therefore conditional independence will imply unconditional dependence. Now let us assume that the index terms are indeed conditionally independence then we get the following remarkable results.
Kendall and Stuart[26] define a partial correlation coefficient for any two distributions by
|
|
|
137 |
|
|
|