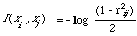where [[rho]] (.,./W) and [[rho]] (.,.) are the conditional and ordinary correlation coefficients respectively. Now if X and Y are conditionally independent then

[[rho]] (X, Y/W) = 0

which implies using the expression for the partial correlation that

[[rho]] (X, Y) = [[rho]] (X, W) [[rho]] (Y, W)

Since

| [[rho]] (X, Y) | <= 1 , | [[rho]] (X, W) | <= 1 , | [[rho]] (Y, W) | <= 1

this in turn implies that under the hypothesis of conditional independence

| [[rho]] (X, Y) | < | [[rho]] (X, W) | or | [[rho]] (Y, W) | (**)

Hence if W is a random variable representing relevance then thecorrelation between it and either index term is greater than the correlation between the index terms.

Qualitatively I shall try and generalise this to functions other than correlation coefficients, Linfott[27] defines a type of informational correlation measure by

rij = (1 - exp (-2I (xi, xj) ) )[1/2]0 <= rij <= 1

or

where I (xi, xj) is the now familiar expected mutual information measure. But rij reduces to the standard correlation coefficient [[rho]] (.,.) if (xi, xj) is normally distributed. So it is not unreasonable to assume that for non-normal distributions rij will behave approximately like [[rho]] (.,.) and will in fact satisfy (**) as well. But rij is strictly monotone with respect to I (x,i, xj) so it too will satisfy (**). Therefore we can now say that under conditional independence the information contained in one index term about another is less than the information contained in either term about the conditioning variable W. In symbols we have

I (xi, xj) < I (xi, W) or I (xj, W),

where I (., W) is the information radius with its weights interpreted as prior probabilities. Remember that I (.,W) was suggested as the measure of discrimination power. I think this result deserves to be stated formally as an hypothesis when W is interpreted as relevance.

Discrimination Gain Hypothesis: Under the hypothesis ofconditional independence the statistical information contained in oneindex term about another is less than the information contained ineither index term about relevance.