

 |
Vandin Lab |
 |
Our research interests are in computational methods for molecular biology, with a focus on problems involving massive data sets. We design of efficient and mathematically well-founded algorithms to solve problems that arise in the analysis of massive biological data, such as the ones produced by next-generation sequencing technologies. While our primary focus is computational biology, we are also interested in other areas involving big data, such as data mining and large network analysis.
Cancer is a disease caused mainly by somatic mutations: changes in the DNA sequence that accumulate during the lifetime of an individual and that are not inherited from parents. A major challenge in analyzing these mutations is to distinguish the few functional driver mutations important for cancer development from the much larger number of random passenger mutations that are not related to the disease. It is widely accepted that cancer is a disease of pathways (groups of interacting genes) and it is hypothesized that driver somatic mutations target genes in a relatively small number (6-10) of signaling and regulatory pathways, each containing a number of genes. Therefore there are myriad combinations of alterations that cancer cells can employ to perturb the behavior of these key pathways. We have been working on methods that rely on different properties of the data to identify driver mutations or mutations important for cancer.


|
HotNet: Discovering Significant Mutated Subnetworks.
We considered the problem of identifying subnetworks (pathways) of a large scale gene and protein interaction
network that are mutated in a significant number of cancer samples, by combining interaction and mutation data.
We designed efficient methods, called HotNet, to identify significantly mutated subnetworks by using a heat diffusion process on graphs to capture graph topology and mutation frequencies/scores, without restricting to predefined subnetworks and/or significant
mutations. Crucial to our methods is an efficient statistical test that estimates the statistical significance of the identified subnetworks by bounding the False Discovery Rate (FDR - the expected ratio of false discoveries among the subnetworks flagged as significant by the method) of the discovered subnetworks. HotNet has been used in a number of publications from The Cancer Genome Atlas (TCGA), and also a study on prostate cancer.
Related publications
|
|
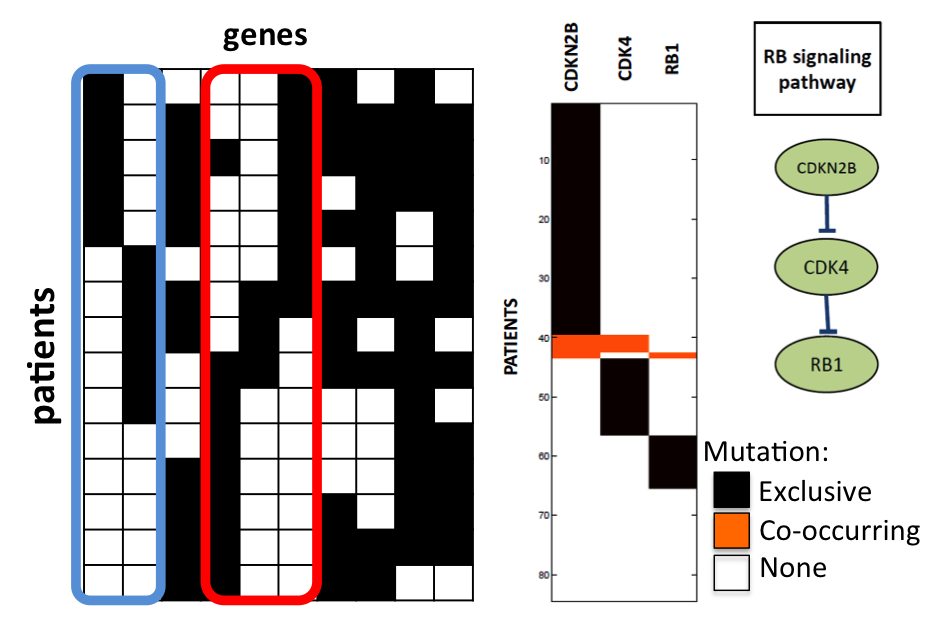
Dendrix: De Novo Driver Exclusivity.
Another approach to identify sets of genes containing driver mutations is to look for gene sets containing specific patterns of mutations. To this end we have designed Dendrix (De Novo Driver Exclusivity) that uses two combinatorial properties, coverage and exclusivity, that distinguish sets of driver mutations from sets of passenger mutations. We have used Dendrix to analyze sequencing data from three cancer studies. In all three datasets
Dendrix finds sets of genes that are parts of pathways known to be important in cancer. We have also studied the theoretical limits of this approach, by considering two generative models for mutations
in cancer and used them to analytically compare Dendrix with the most commonly
used method to identify significantly mutated genes. We proved that our methods are more robust than the standard method to noisy in the data.
Related publications
|


|
Accurate Genome-Wide Survival Analysis.
Deriving clinical utility from genomic datasets requires the identication of statistically signicant associations between genomic measurements and a clinical phenotype. An important instance of this problem is to identify genetic variants that distinguish patients with different survival time following diagnosis or treatment. The most widely used statistical test for comparing the survival time of two (or more) classes of samples is the nonparametric log-rank test. Nearly all implementations of the log-rank test rely on the asymptotic normality of the test statistic. However, this approximation gives poor results in many high-throughput genomics applications where: (i) the populations are unbalanced; i.e. the population containing a given variant is signicantly smaller than the population without that variant; (ii) one tests many possible variants and is interested in those variants with very small p-values that remain signicant after multi-hypothesis correction. We develop and analyze a novel algorithm for computing the p-value of the log-rank statistic for any range of population sizes under the exact permutational distribution, and we demonstrate the practicality and accuracy of our approach analyzing somatic mutations and survival data from The Cancer Genome Atlas project.
We also worked on generalizing HotNet to discover subnetworks of a large interaction network containing mutations associated with survival time. Related publications
|
We have worked on detecting common patterns (motifs) in biological sequences, and in 3-dimensional protein structures. The analysis of protein sequence-structure-function relationships is crucial, since it enables the prediction of functional characteristics of new proteins, provides molecular-level insights into how those functions are performed, and supports the development of variants that specifically maintain or perturb the function in concert with other properties.

|
MADMX: Maximal Dense DNA Motifs.
We studied the problem of extracting motifs with errors from biological sequences. Due to computational reasons, previous methods either did not bound the number of errors at all or required a fixed (small) upper bound on the number of errors for the motifs. In the first case, a huge number of ``trivial'' motifs containing a large fraction of errors, and therefore not useful, are reported, while in the second case it is impossible to set an upper bound that is meaningful for both short and long motifs. In we introduced density, a simple and flexible measure for bounding the fraction of errors in a motif, and developed, analyzed and implemented a new algorithm (MADMX), which extracts maximal dense motifs, possibly including errors, that occur above a user defined threshold. We provided experimental evidence of the efficiency of our algorithm and of the quality of the motifs returned by our algorithm on real data.
Related publications
|

|
BALLAST: Structural Motifs Matching.
Structural (3-dimensional) motifs encapsulate the common characteristics of a set of (related) proteins. Previous methods reduced the problem of finding structural motifs to NP-hard graph problems or to seed-and-expand methods combined with a computationally expensive exhaustive search for seeds. We designed a simple, general, efficient approach to match a given structural motifs to given protein structures, based on the direct combination of the geometrical and chemical components of the problem. We provided analytical and experimental evidence of the efficiency of our algorithm, proving its efficiency when the data comes from a probabilistic model and testing it on real and simulated data, and we demonstrated its ability to discover motifs previously determined by experimental and expert analysis.
Related publications
|

|
This is a fundamental primitive for market basket analysis and several other
commercial and scientific big data applications. A recent variation of the problem requires to extract the K most frequent (closed) itemsets, or top-K frequent (closed) itemsets; this variation aims to better control the output size, that cannot be effectively predicted in the original definition of the problem. We provided the first analytical evidence of the effectiveness of the approach and also designed and implemented an efficient algorithm, TopKMiner, for the incremental mining of top-K frequent closed itemsets in order of decreasing support, which exhibits consistently better performance than the best previously known one. We also studied the use of sampling for the extraction of the top-K frequent itemsets, a problem
that was not well studied before. We developed an algorithm to efficiently extract the top-K frequent items/itemsets through progressive sampling and using a variation of Bloom filters, and showed experimentally the efficiency and accuracy of our method. Furthermore, we studied the extraction of significant itemsets.We developed a novel methodology to identify a meaningful frequency threshold for a dataset, such that the
frequent itemsets with respect to can then be flagged as statistically significant with a small False Discovery
Rate (FDR). We provided analytical and experimental evidence of the effectiveness of our approach, testing it on real and simulated data.
Related publications
|

|
We studied graphs problems in settings where the graph changes over time, and the algorithm can only observe these changes by probing the graph in a limited way. A motivating application for this framework is given by algorithms on decentralized networks such as the Internet or social networks. The data that such algorithms must work on is an actual network, which can change over time without notifying the algorithm. The fact that the algorithm is unaware of the changes in the input makes this setting different from a typical setting in dynamic algorithms, where the algorithm is informed of the changes in the data. We focused on basic graph algorithms in this framework. Besides developing a formal model, we studied two fundamental problems: finding paths and minimum spanning trees. We gave almost tight positive results on both problems, showing how to maintain good approximate solutions over the time.
Related publications
|